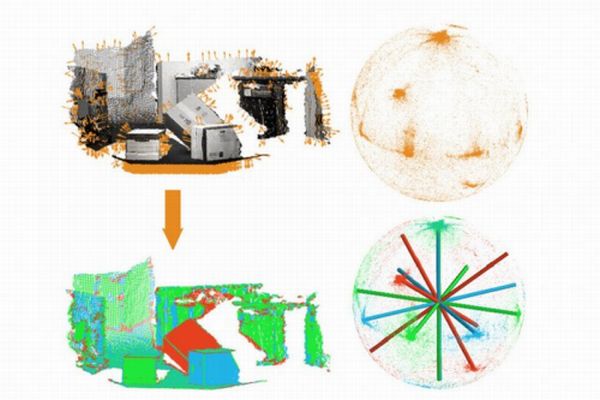
Re-orientation of scenes and multi-target tracking are the fundamental problems for majority of vision applications. Occlusions and slight change in scene alignment make tracking by detection approaches a lot more challenging.
Thinking on the same lines, MIT researchers have come up with a new algorithm that would assist the vision applications in combating the re-orientation problems. The algorithm is chiefly written for bots and machines that are employed for navigational purposes.
Manhattan Frames
The mechanism is based on recognizing the main orientations in the given scene. These alignments act as sets of axes inserted in a sphere. These axes have been named as Manhattan frames. Now as the bot moves, the sphere spins in a particular direction, and so the bot observe the orientation, which is relative to the axes. Thus, keeping a record of the landmarks each time when there is shift in the relative alignment, the robot is never lost of its mission or the target.
The same algo also helps in simplifying plane segmentation, which means, ability to visualize surroundings in 3 dimensions. In humans, a similar technique is called the depth perception.
Sensing & Learning of the Surroundings
Points that are formed on the set of axis (inside the sphere) are calculated in terms of their orientation. Each placement defines a unique inclination with respect to the sphere’s center.
The initial alignment is based on approximation because of which it becomes difficult to make out the points. However, with the help of statistical data regarding the vagueness of the primary orientation estimates, the algorithm then tries to adjust Manhattan frames to the points on the sphere. The method is quite similar to that of regression analysis.
Freifeld one of the lead researcher asserted that the algo takes into consideration of the geographical distances and converges these geometries with statistical reasoning about the scene. Conventionally, measuring the statistical distance between the two places will give sum between the places or an average of the two. But the same does not work for nonlinear spaces. For instance, measuring distance between Tokyo and New York will not give the desired output as per classical statistics but the new algorithm has an answer for this problem.
Researchers envision that this technique will revolutionize the autonomous systems, including household robots or self-driving cars but it will solely depend on the implementation and deployment of these techniques by the companies.