I’ve been thinking a lot about how deep neural networks actually learn. I mean, those complex stacks of layers, how do they figure out the mechanics to recognize images or understand speech? These layers must be working together to make sense of raw data, but how?
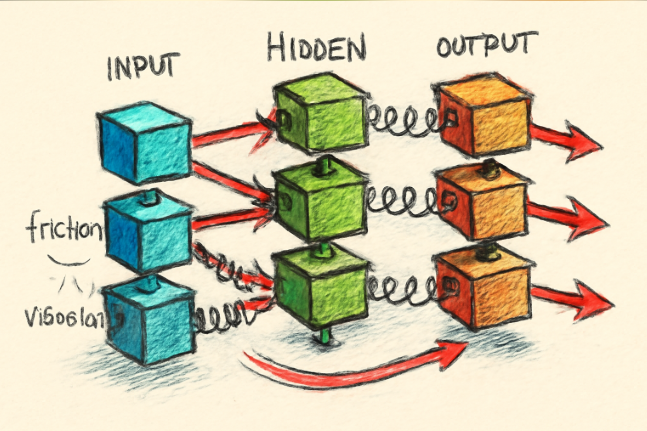
Recently, I came across this analogy that really cleared things up for me, it goes like this, each layer is a block connected by springs. So, the amount each spring stretches is how much that layer/block “improves” the data, like making apples easier to separate by color. So instead of tearing our brains trying to understand every single neuron, we just focus on how the whole chain behaves.
The study is published under the title, Spring-Block Theory of Feature Learning in Deep Neural Networks.
Spring-Block Analogy for Deep Neural Networks
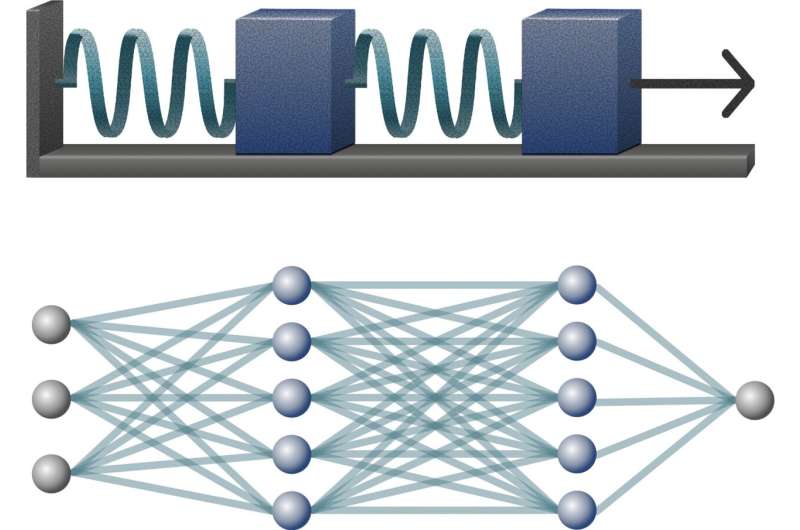
Researchers use this spring-block model to explain how DNNs learn features and progressively separate data across their layers, drawing parallels between the mechanical behavior of a chain of blocks connected by springs and what happens computationally inside a neural network.
Here’s the breakdown of this analogy:
- DNN Layers as “Blocks” in the System: Just like a spring-block chain has blocks connected layer by layer, a deep neural network is structured in layers. Each layer transforms input data into features that guide the next layer’s processing.
- Data Separation as Spring Extension: The “stretching” of each spring corresponds to how much a layer simplifies or separates the input data. This data separation is quantified by the ratio of feature variance within and across classes, basically, how well a layer improves data representation. The difference in data separation between consecutive layers shows the contribution of each layer, much like how much each spring elongates.
- Nonlinearity as Friction: Nonlinearity inside a neural network is like friction between the blocks and the surface in the mechanical system. This friction resists block movement, or in the neural net, it absorbs load or spoils gradient signals, meaning shallow layers may “stretch” less or learn less effectively. Importantly, this friction isn’t symmetric; it models how noise propagates differently during training.
- Training Loss as a Pulling Force: The network’s training loss, the request to explain observed data, acts like a pulling force applied to the last block in the chain. This force causes the blocks (layers) to separate, progressively improving data representation layer by layer.
- Noise as Vibrations or Shakes: Noise in training (from things like small batch sizes, dropout, label noise, or learning rate fluctuations) corresponds to vibrations or shakes in the spring-block chain. These shakes help rebalance the load across the springs (layers), allowing earlier layers to contribute more by “loosening” friction and equalizing feature learning.
- Data Flow and Gradient Propagation: In a real DNN, input flows forward from shallow to deep layers, and gradients flow backward. The asymmetric friction in the model captures how noise (especially dropout noise) mostly propagates from shallow to deep layers, making the gradients in the deepest layers the noisiest.
How Nonlinearity & Noise Shape Feature Learning
What surprised me is how the shape of this “load curve” depends on two things. Basically, the “load curve” means how much each layer contributes. The two things are:
- How nonlinear the network is
- How noisy the training process gets
What does Nonlinearity & Noise mean?
1) Nonlinearity, here is, like friction. When it’s high, the early layers get stuck and don’t learn much. That means the early layers aren’t doing much, so the deeper layers have to compensate, they end up stretching their springs a lot. The load curve bows downward, like a concave shape.
Let’s say, you and a friend are carrying a heavy couch. If your friend in the front slips and can’t carry much weight, you’re forced to take almost all of it at the back. That’s what high nonlinearity does, it forces the back of the network (deep layers) to do most of the work.
2) While noise is like giving the whole chain little random shakes while it’s learning. In a real neural network, this “shake” comes from things like using small batches of data, adding dropout, or even having random variation in the input.
In absence of noise, each block only moves when there’s a clear, strong pull from the layers before it. Sometimes this means the early layers just sit there almost still, while deeper layers do most of the stretching. And when noise goes up, it pushes the load curve into a convex shape, meaning early layers start learning better features.
For instance noise is like stirring a pot of soup while tasting it.
- If you never stir, the flavors in some parts stay the same for a long time, and you only notice changes when you reach the deeper layers of the pot.
- If you stir a little as you go, every part of the soup gets mixed and adjusted, so the flavor improves everywhere, not just at the bottom.
Takeaway: Try Adding Noise If Layers Are Struggling
This gives a practical tip for training networks. If you notice your network’s load curve looks concave (with deeper layers doing most of the work), try adding more noise, like increasing dropout or lowering batch size. It can help “flatten” the learning distribution and improve how well the network generalizes.
The best part of this approach is how it simplifies something that usually feels so complicated. Instead of tweaking dozens of parameters blindly, you have a straightforward way to diagnose and fix learning imbalances.
I’m curious though, how would you check the load curve on your own model? And do you think this analogy holds up for different architectures like transformers, or just the usual convolutional networks?
It feels like understanding learning this way might save a lot of trial and error. And it definitely changed how I think about tuning deep networks.
Source: Phys.org