
James Gleick is a prolific author and essayist renowned for his insightful exploration of the intersection between science, technology, and their profound cultural impacts.
In “Chaos: Making Sense of a Complex World,” he introduces us to a world where order arises from apparent disorder. It was first published in 1987.
The book invites us to contemplate the rigid lines and shapes of man-made structures and the organic irregularity found in nature. This introspection gives rise to the fundamental question:
What is it behind the exquisite and elusive nature of chaos in natural systems?
Chaos theory, as explained by Gleick, has the answer for the conundrum. It claims that complex systems in nature have some universal order. And this order leads to surprising and often unpredictable outcomes.

Fractal Geometry a Tool to understand Complex Systems
Animate and inanimate objects, like jellyfish, ink dropping in water, lightning’s, and trees’ branches both exhibits strikingly similar patterns.
According to Gleick, if one wants to understand these patterns, one needs to have some kind of tool. And so, he introduces fractal geometry, a tool essential for understanding these intricate systems.
“The insights of fractal geometry helped scientists who study the way things meld together, the way they branch apart, or the way they shatter. It is a method of looking at materials—the microscopically jagged surfaces of metals, the tiny holes and channels of porous oil-bearing rock, the fragmented landscapes of an earthquake zone.”
Unlike the familiar Euclidean geometry with its lines, rectangles, and circles, fractal geometry mirrors the irregular shapes.
Nature is saturated with these geometries. For instance, we have clouds, birds, trees, flowers, fruits, and seashores to name a few. And fractal geometry gives us the lens through which we can see the geometries and make something out of it.
Aperiodicity and Unpredictability
While tracing the roots of chaos theory, Gleick acknowledges the works of Edward Lorenz. He uncovered the butterfly effect and explored the relationship between aperiodicity and unpredictability.
Aperiodicity can contribute to unpredictability when it makes it challenging to discern a clear pattern. In simple words, if a system lacks regularity in its dynamics, it becomes difficult to project its future states.
While the butterfly effect is a concept that suggests that even miniscule events or changes in one part of a complex system can have far-reaching and unpredictable consequences in another part of the system.
Thus, highlighting the sensitivity of complex systems to initial conditions. And the difficulties that the system face while predicting the behavior over time.
Chaotic Aspects within Living Organisms
Another interesting idea that challenges conventional wisdom, is the chaotic aspects within living organisms. As mentioned above, small changes in the starting state of any system can lead to drastically different outcomes over time. And when it comes to living organisms, chaotic behaviour serves as a self-defending system.
For instance, unpredictable firing of neurons (within an organism’s nervous system) can lead to unpredictable and flexible behaviors. This adaptability leads to fight or flight mode.
Similar chaotic behavior within the immune system assists in responding to a wide range of pathogens and threats.
Seemingly random or irregular behaviors are driven by underlying deterministic processes. Phenomenon includes, irregular movements of eye muscles and blockage of blood vessels in an organism.
Tiny variations or fluctuations in the state of blood vessels, for instance, could result in different patterns of blood flow or even occasional blockages.
History and Concepts Surrounding Chaos Theory
The book also explores some concepts surrounding chaos theory. Following are some of the interesting observations.
- John Yorke is credited with coining the term “chaos”. His dual expertise as a mathematician and philosopher helped gained essence of chaos theory. In addition, it reflected the interdisciplinary nature of chaos theory.
- Steve Smale, an illustrious mathematician in his own right, left an indelible mark on the unfolding narrative of chaos theory. He was amongst the luminaries who shaped this dynamic field. He delved into the realm of topology, a captivating branch of mathematics that probes the enduring characteristics of geometric objects. He unveiled the enduring properties that withstand the tests of distortion, contortion, and expansion.
- Benoit Mandelbrot’s exploration of fractal geometry is celebrated for its pivotal role in chaos science. It was because of him fractal geometry and chaos theory could find a common ground.
- Swinney and Gollub demonstrated the concept of transition from order to chaos in fluid dynamics. They worked on fluids in a cylindrical container which was subjected to rotation. When they rotated the container, torus-shaped pattern (of the fluid) began to emerge. As they progressively increased the speed of rotation, new frequencies and patterns started to manifest within the fluid dynamics.
At a certain threshold of rotation speed, the orderly pattern abruptly disintegrated. Thus, giving way to a state of complete and unpredictable chaos within the fluid.
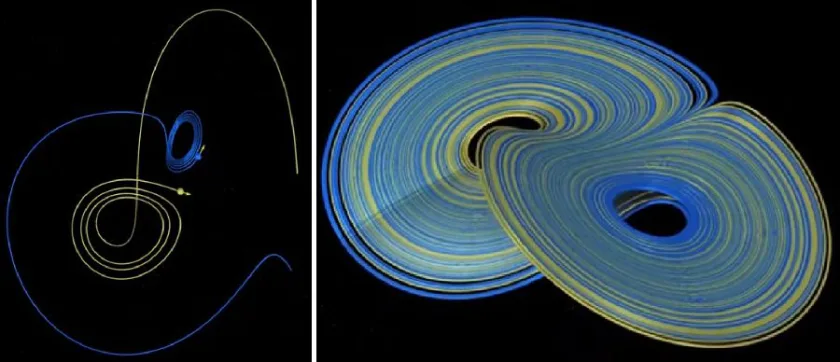
Strange Attractors’ Orderliness and the Fractal Connection
I’d also like to point out another interesting analysis made by Gleick regarding strange attractors.
Strange attractors in chaotic systems exhibit some orderliness in their orbital behavior. However, this orderliness is different from the regular, repeating patterns seen in non-chaotic systems.
What are strange attractors?
Strange attractors have a complex and intricate structure. beautiful patterns of loops and spirals
These attractors are the regions within a system’s phase space that chaotic trajectories tend to approach and remain within.
Although, they exhibit some orderliness in the sense that they have a distinct structure, they are also characterized by sensitivity to initial conditions. This implies that “nearby trajectories” can diverge over time.
“Nearby trajectories,” means that if you start two initially very close points within a chaotic system, their subsequent paths or trajectories will initially appear similar because they are close. However, due to the sensitivity (as mentioned earlier), these trajectories will gradually diverge and become significantly different over time.
Therefore, the connection between chaos theory and fractals lies in their shared characteristics of complexity, self-similarity, and the manifestation of intricate patterns within seemingly finite spaces.
These characteristics makes them deeply connected and valuable tools for exploring and explaining the complexity of the natural world.

Takeaway
From cosmos, to natural ecosystems, and finally to the intricacies of the human anatomy, chaos theory exhibits its expansive versatility. Overall, “Chaos: Making a New Science” is an interesting exploration of chaos theory.
The idea that everything in the universe is broken down into patterns mirrors the “quarks” sentiments of quantum physics. If this is correct then it strongly implies that universe is fundamentally governed by some underlying mathematical laws. And therefore, it can be discovered and described through scientific inquiry. Of course, persistence and resilience will be the key in the journey of scientific exploration.
At the same time, it is important to recognize that the universe is also characterize by inherent complexity and emergent phenomena, which is yet to be conceived by human understanding.



[…] James Gleick, one of my favorite science writers, wrote this famous quote in his book Chaos: Making a New Science: […]