
Gödel, Escher, Bach: an Eternal Golden Braid by Douglas Hofstadter was first published in 1979. Famously known as GEB, the book touches upon everything – consciousness, self-reference, computer science, formal systems, proofs, mathematics, abstract structures, codes, language, music, storytelling, conversations etc.
At the beginning, I’d like to mention that I’m not qualified to review this book, as I lack a background in mathematics. Despite my difficulty in understanding complex concepts, from what little I’ve grasped, I believe this is one of the most profound works I’ve encountered so far.
Having said that, this book provides several compelling reasons that reinforce my position as an agnostic. Some of which are:
- One, no system is perfect, every system has limitations.
- Two, as an individual, we will never gain/acquire “all” the information, some part of information (across systems) will always remain hidden from us.
- Three, human knowledge will always be limited, be it the nature of mathematical truth or the origin of universe or what is behind quantum fluctuation or ultimately, the question of what we are.
Also, I find that the notion of symbols, structure and self-reference mentioned in the book can be extended to religions across the globe.
The book illustrates how symbols in language, codes or mathematics hold no inherent meaning. It is the mind or people that assign meaning to these mechanistic symbols. In the context of religion, these symbols are often elevated to the status of being “holy”. What any symbol mean to an individual is directly proportional to the person’s perceptions, beliefs and self-reference, which is the result of religious doctrines, hard wired in people’s DNA.
Exploring Achilles and the Tortoise
After each chapter, the book has this super interesting conversation between Achilles and the Tortoise, I thoroughly enjoyed those. In fact, I see these sections as a reward, something to look forward to after engaging with the more complex concepts in each chapter. They add a refreshing and insightful break from the technical material.
This review is more like a collection of my notes on each chapter. The book is divided into two parts:
- Part I: Contains chapters 1 to 9
- Part II: Covers chapters 10-20
This post is only about part 1 of the book. And I will upload the rest of the notes once I finish reading the entire book. So, let’s begin with first chapter.
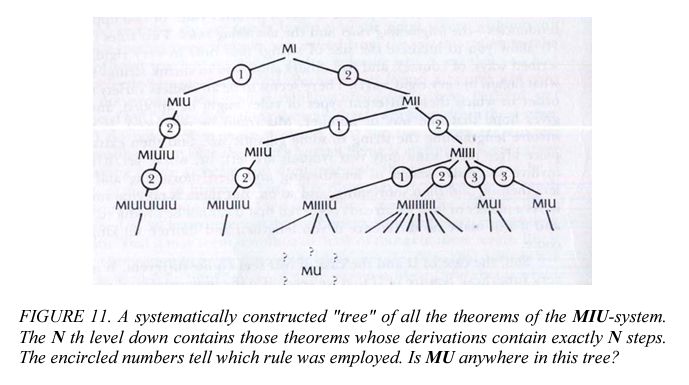
Chapter I: The MU-Puzzle
Hofstadter starts the book by introducing us with the basic concept of how formal system works. Every such system has three main features – starting point, rules (that operates within the system) and the end goal. Thus, the entire operation of that system has its own logical processes.
To make things understandable, he lays an example of MU-puzzle. The aim of the riddle is to exchange letters “MI” into “MU”, with the given set of rules. When all the permutations and combinations are applied, it is realised that it is just not possible to converge to such an end. This means, there is an inherent limitation in the formal system. With this thought experiment, the author lays the ground work for self-reference, paradoxes, and Gödel’s incompleteness theorems.
Second half part of the chapter is a structural discourse between, Achilles and the Tortoise – the famous characters inspired from Lewis Carroll’s “What the Tortoise Said to Achilles” (1895). The crux of the conversation can be divided into following three parts:
- Logical paradox: Just because two people (Achilles and Tortoise) agree on some things (A and B) that logically connect to the obvious conclusion (C), it doesn’t mean both have to agree to the final idea (Z). There is a possibility of having an extra statement (D), which is if A, B, and C are true, then Z has to be true as well. Thus, the new statement keeps on adding with each confirmation of the earlier statements.
- Infinite regression: The above logical paradox leads to infinite regression or an endless loop of needing more and more confirmations.
- Absurdity of formal proofs: The never-ending series of justifications, in theory, causes one to caught up in an endless loop of needing more and more reasons to back it up.
This, according to Hofstadter, highlights the problem in strict logical systems. Even if the conclusion is right in front of it, the subsequent rhetorical questions can spiral into an infinite series of justifications, without actually getting to a final answer.

Chapter II: Meaning and Form in Mathematics
The next chapter talks about connection between symbols, meaning, and structure within formal systems, particularly in mathematics. With an example of “pq-system”, invented the author himself, he puts forth the idea that how meaning emerges from interplay of purely mechanical process of symbol manipulation. To simplify further, he argues, with the help of certain rules, (which operates within the system) variables can be operated without any reference to what they “mean”.
Inherently, the symbols and rules do not have any meaning, so, the workings of the system are purely based on syntactic rules. This implies that the meaning, which is derived later is nothing but an additional layer applied to the system. In his own words,
“When you confront a formal system you know nothing of, and if you hope to discover some hidden meaning in it, your problem is how to assign interpretations to its symbols in a meaningful way-that is, in such a way that a higher-level correspondence emerges between true statements and theorems.” (pg.62)
The chapter also culminates with conversation between Achilles and Mr. T. The discussion surfaces some of the abstract ideas, such as:
- Achilles refers to how J.S. Bach played sonata on the fly. And he marvels at his talent of creating complex music with a single violin.
- Mr T, however, is distracted with “ADAC” puzzle.
- The conversation then shifts to M.C. Escher’s artwork “Mosaic II”. It is a visual concept where our mind tries to make sense of objects from the background. With this idea, Hofstadter wants us to experience how puzzles can be interpreted in a complex environment. The end goal of this exercise is to find some hidden meaning.
Lastly, they conclude that Bach’s sonata has only solo instrument, his violin. The characters speculate that listeners can mentally construct additional layers of music, for instance, an accompaniment of a harpsichord. This conclusion hints at how one can find deeper meanings in complex systems, puzzles and art (music) by one’s own subjective process of understanding.

Chapter III: Figure and Ground
This chapter is dedicated towards surfacing the combination of foreground and background, both in – visual arts and logical structures. The author uses M. C. Escher’s famous painting “Tiling of the plane using birds” to describe how our perceptions shift between “figure” and “background” in the same single image. There are also references to Escher’s other such paradoxical drawings.
This idea of revealing meaning in structures, systems, or in a particular environment surface how our observation is perception and hence, subjective based. This equation leads to broader idea of self-reference.
Hofstadter extends this notion in mathematics and formal systems, by laying similar comparison between theorems (provable statements) and non-theorems (unprovable statements).
Finally, there comes the dialogue between Achilles and the Tortoise. This time, the Tortoise narrates a story about his friend, the Crab, who was sure that his phonograph could play any type of music. To this, the Tortoise created a record, which was called “I Cannot Be Played on Record Player 1”. This record led to the phonograph to break. This eventuality circled again and again as the Crab bought increasingly expensive and supposedly perfect phonographs. These events, as per author, highlights Gödel’s Incompleteness Theorem.

Chapter IV: Consistency, Completeness, and Geometry
Chapter four talks about the consistency and completeness of formal systems. If a system does not give rise to any contradictions, that is, there is no proving or dis-proving anything, it will form a consistent system. For example, 2+2=4 and all right angles would have to be congruent etc.
If a system is complete, which is, if every statement is true within its domain, it will be termed as complete system. For example, Euclidean geometry (Statements about points, lines, and planes can be either proven or disproven using the axioms and rules of inference of Euclidean geometry.)
Hofstadter claims that both concepts give center stage to – Gödel’s Incompleteness Theorem. How?
It states that for any powerful system, achieving completeness and consistency simultaneously is impossible. For instance, Lobachevskian geometry and Riemannian geometry, challenge the axioms of Euclidean geometry. Consider the following examples:
- Angles within a triangle drawn on a flat surface will always add up to 180 degrees. This falls under the traditional Euclidean geometry.
- Angles of a triangle drawn on the surface of a balloon will always add up to more than 180 degrees because of the surface curves. This is the world of Riemannian geometry.
- Angles of a triangle drawn on the surface of a saddle will always add up to less than 180 degrees because of the saddle’s inward curves. This is the Lobachevskian geometry.
The subsequent portion of Tortoise and Achilles moves in form of a story. Both ride the Ferris wheel at Coney Island. From here their adventure starts – they get kidnapped, read books, consume potions to enter the picture world of “Convex and Concave”, retrieves the magic lamp from two lizards, asks for “meta-wishes” from genie, which causes paradox and they fall into a limbo for dormant software (after the crashing of their world). Then they explore a musical maze followed by a labyrinth, there they eat popcorn, and return to normal size.

Chapter V: Recursive Structures and Processes
Chapter five explores that concept of recursion. It is a process that leads to looping structures like Fibonacci sequence, which shows how simple recursive rules (the next term in a sequence from the previous term) can generate complex outcomes.
As per the author, recursive nature not only demonstrates itself in mathematics but it is also a fundamental concept in computer programming (chess), language (grammar and syntax), music and in Escher’s Art. With this Hofstadter illustrates how recursive processes form the basic foundation of self-reference and infinity.
In the segment of Tortoise and Achilles, both are seen sitting in a Chinese restaurant and discussing the concept of haiku. Achilles then finds fortune cookie and both tries to decode the meaning of letters. They conclude that meaning has an ambiguous nature as it is subjective to individual perspective.
Then they talk about interval patterns in music, such as, “B-A-C-H” and “C-A-G-E” share a common structural pattern based on interval multiplication. And how it generates complex patterns through repeated application. This mirrors themes of recursion and self-reference.

Chapter VI: The Location of Meaning
The next chapter begins by establishing the fact that symbols inherently do not have any meaning. They are mere words or elements in a formal system (similar idea was also mentioned in Chapter II). Only in presence of a mind, these symbols can be interpreted in a specific context.
Hofstadter says that various systems have multiple levels of meaning. These meanings are an offshoot of manipulation of symbols. Extending the equation, he claims that meaning necessarily is not only a matter of representation but also of interpretation. For instance, artificial systems like computers do not understand the symbols or the words as humans do but they can manipulate those symbols as per the rules.
The chapter concludes with the idea that how meta-language can add another layer to the complexity of meaning. Meta-language here refers to a type of language used to talk about or analyze another language. So, syntax and grammar (tools for meta-language) also contribute in how meaning is constructed and interpreted.
Now comes the interesting conversation between Tortoise and Achilles, all rich with wit and humour. It starts with Achilles commenting on Tortoise’s shell’s color, which is green. But the Tortoise evades this by playing with the ambiguity of language. He says, it’s both – that his shell is green and that it is not. He justifies his stance by pointing out that apparent contradiction may not be so under different interpretations of words or contexts. This shows that although logic and language are the biggest tools to understand any system, but they also have some inherent pitfalls and complexities.

Chapter VII: The Propositional Calculus
The chapter VII starts with the explanation of Propositional Calculus. It is a formal system that deals with the statements, which can be either true or false. These propositions can be combined using logical operators (also called connectives) like:
- AND ( ∧ )
- OR ( ∨ )
- NOT ( ¬ )
- IMPLIES ( → )
As always, in this system also, complex statements are constructed from simpler ones. The aim of this exercise is to abstract reasoning into a symbolic form. However, in here, logics can be manipulated systematically. Therefore, if the rules are applied correctly, every theorem derived within the system is guaranteed to be true, also called the Truth-Preservation.
In case of an individual proposition, by listing all the possible scenario for its simpler parts, one can figure out whether a complex statement is true or false. For example, the statement:
- “If it is raining, then the ground is wet” (rain → wet) is logically equivalent to “It is not the case that it is raining and the ground is not wet” (¬(rain ∧ ¬wet)).
Through this, Hofstadter demonstrates how reasoning can be reduced to syntactic manipulation of symbols. This idea resonates with the theme of the book, which is, formal systems can model not only mathematical reasoning but also processes like computation and (mind) thought.
The author then takes us to David Hilbert’s idea as per which, all forms of mathematics can be converted to a set of axioms and rules that could be mechanically followed. Propositional calculus (presented above) is the first step towards the trajectory.
This idea links to Hofstadter’s broader exploration of whether complex thought, like human cognition or self-reference, can be captured by formal systems. In the above context, the propositional calculus tells us how to manipulate symbols, but it doesn’t care about what the symbols mean. So, the question presents itself- can meaning arise from purely formal rules?
This links to one of the book’s main themes: whether minds and consciousness, which seem rich with meaning, might also emerge from purely mechanical systems following rules.
The chapter culminates with a paradoxical conversation between Achilles, the Tortoise, and the Crab. After exchanging greetings, Achilles and Tortoise praise each other. Tortoise then offers Achilles a cigar, leading to a humorous debate on the quality of Dutch cigars. Followed by debates on their preferences for Bach and Escher, invoking the Latin phrase “De gustibus non est disputandum” (There’s no disputing about taste). The conversation contains several puns and plays on words, especially regarding “fret” (musical frets vs. worries) and “Pole” (a person vs. a guitar-related pun). For instance, Tortoise asks Achilles if being his age means having no worries, leading to a light-hearted exchange about frets and worries.
The conversation has no conclusive ending but serves to highlight playful reasoning, paradoxes, and self-referential humour in a structured form.

Chapter VIII: Typographical Number Theory
In Chapter VIII, Hofstadter introduces us to Typographical Number Theory (TNT). In the book, TNT is a reworking of Peano Arithmetic within the framework of formal logic. Peano Arithmetic (PA) is a formal system (in mathematical logic) used to define the properties of natural numbers (0, 1, 2, 3, …). It provides a set of axioms that describe the basic properties of the natural numbers and arithmetic operations like addition and multiplication.
TNT is essentially Peano Arithmetic written as a formal system, i.e., the meaning of the symbols is determined purely by the rules and axioms. Hofstadter illustrates how TNT translates familiar arithmetic statements in symbolic form. For example, the statement “1 + 1 = 2” can be written in TNT’s formal language using special symbols and rules.
The chapter goes deep into how this symbolic system can represent increasingly complex ideas, including simple arithmetic equations, inequalities, and even deeper number-theoretic truths.
Finally, the author talks about the Gödel numbering, which is super important for Gödel’s incompleteness theorem. As per Gödel numbering system, each component in TNT is assigned a unique natural number. The components include:
- symbol
- formula
- proof
This allows us to represent statements about the system itself (metamathematical statements) as numbers. This implies that TNT statements is a form of self-reference because it talks about itself. This capacity is the key ingredient in Gödel’s proof that there are true statements within the system that cannot be proven using the system’s rules (Gödel’s incompleteness theorem).
Let’s say a certain TNT system is 1 if “This statement is true”. Now, if we have another statement that says “The statement represented by the number 1 cannot be proven true by the machine.” According to Gödel’s theorem, while the first statement may be true, the TNT system cannot prove the truth of the second statement using its own rules. This illustrates that there are true statements that remain unprovable within the system.
Now comes the interesting conversation between Achilles and Tortoise. Achilles dozes off during a lecture and imagines DNA represented by himself and Tortoise, as a double helical structure. On getting stuck over molecular biology’s strange loops and complexities, he starts talking about Zen Buddhism to escape analytic thought. The conversation moves around nonattachment, the quest for enlightenment (Satori), and the significance of koans as tools for understanding and transcending intellectual thought. The discussion hints at just like koans, geometric symbols too represent the process of transforming abstract concepts into tangible forms. This implies that true understanding transcends Zen teachings and the inherent complexity of philosophical ideas and rely instead on experience and insight.

Chapter IX: Mumon and Gödel
Chapter IX talks about the relationship between Zen Buddhism, logic, and mathematics. The author starts with the idea of how Zen koans challenges conventional thinking. The chapter presents paradoxical anecdotes in form of poems, conversations and riddles used in Zen practice, like:
The student Doko came to a Zen master, and said: “I am seeking the truth. In what state of mind should I train myself, so as to find it?”
Said the master, “There is no mind, so you cannot put it in any state. There is no truth, so you cannot train yourself for it.” “If there is no mind to train, and no truth_ to find, why do you have these monks gather before you every day to study- Zen and train themselves for this study?”
“But I haven’t an inch of room here,” said the master, “so how could the monks gather? I have no tongue, so how could I call them together or teach them?”
“Oh, how can you lie like this?” asked Doko. “But if I have no tongue to talk to others, how can I lie to you?” asked the master. Then Doko said sadly, “I cannot follow you. I cannot understand you “I cannot understand myself,” said the master. (pg.258-9.)
Here, Hofstadter is trying to draw parallels between Zen koans and Gödel’s incompleteness theorems. How? Both – Gödel’s theorem and Zen koans – talk about the inherent limitations that are present in structured thought and logic.
Zen koans encourage practitioners to see beyond the constraints of language. And Gödel’s incompleteness theorems demonstrate that in any sufficiently powerful formal system self-referential statements cannot be proven.
In the structure of koans and Gödel’s incompleteness theorems, self-reference and recursion create loops of meaning and understanding. And so, according to the author, both can lead to deeper truths. Zen koans and Gödel’s theorem, suggests Hofstadter, encourage a form of enlightenment. How? As mind tries to step outside of its current framework to have a third party perspective which is not based on self-reference.
The conversation at the end of the chapter between Achilles, Tortoise, Crab, and Anteater is a mixer of mathematics, particularly Fermat’s Last Theorem, with the complexities of listening to music, specifically fugues by Bach.
Achilles and Tortoise start their discussion by saying that no solutions exist for a particular equation, which is, a^n + b^n = c^n for n>2. This is also known as Fermat’s Last Theorem. Interestingly, the author has juxtaposed this impossible feat with historical performance of “retrieving” a recording of Bach playing the harpsichord, which was never recorded. Thus, creating a paradox.
When they listen to a recording of Bach’s “Well-Tempered Clavier”, they end up discussing fugues. A complex musical form where multiple melodies are intertwined. They compare this form with complex systems in mathematics. As Achilles feels torn between focusing on a single voice in the fugue or hearing the whole piece, they conclude how minds try to flip between focusing on details and taking multiple entities together as a whole, whether in music or mathematics.
Over all, the discussion makes one ponder on limits of perception, knowledge, and interpretation, both in mathematics and music.

Takeaway
As I have mentioned in the beginning also, this is not a review per say, but my notes on GEB as I find this book is rich with profound insights and challenging concepts that stimulate my intellectual curiosity. No doubt some of the content is a bit challenging, but the way the author has constructed arguments with proofs and analogies is worth the time spent reading. It took me a month just to finish half (290 pages) of the book.
In a nutshell, this is the greatest mind-expanding book ever written. A huge shout-out to Physixfan for making the PDF of this book available!



[…] you through Gödel’s incompleteness theorems, (I’ve talked about it in my review notes on Gödel, Escher, Bach by Douglas Hofstadter) quantum mechanics, and the possibilities of non-computational processes in human […]
[…] I’ve always enjoyed intellectual challenges. Spending months unraveling Douglas Hofstadter’s Gödel, Escher, Bach was demanding, but deeply […]