“The Symmetries of Things” explores mathematical symmetry and the symmetrical properties of geometric objects. The book was a collaborative effort spanning many years, authored by John Horton Conway, Heidi Burgiel, and Chaim Goodman-Strauss. It was first published in 2008 by A K Peters.
With its exceptional visualization, the book offers fresh perspectives on dimensions, symmetries, and objects, allowing readers to see them in entirely new ways. As I delved into the book, I couldn’t help but envision tessellations patterns swirling in my mind. With each turn of the page, I felt myself drawing nearer to unraveling the hidden symmetries that lie beneath these intriguing designs.
Despite not having a mathematical background, I’ve always found patterns fascinating. Part I was easy to grasp, while Part II and III posed some challenges. Nonetheless, I sensed the influence of Escher-like patterns guiding me and nudging me forward. It really demonstrates the universal appeal and power of patterns. The book is segmented into three parts; let’s delve right into the initial section.

Symmetries of Finite Objects and Plane Repeating Patterns
Part 1 is suitable for all readers. It covers a range of topics including topology, group theory, and orbifolds. Orbifolds are mathematical objects, where symmetrically identical points are folded together. But before that let’s touch on the basic concept of “frieze patterns”, as it is chronologically mentioned in the book.
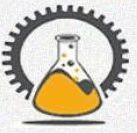
These designs (frieze patterns) are a type of repetitive pattern that can be extended infinitely along a straight line. These patterns are often found in architecture, textiles, and decorative arts. The authors classify frieze patterns into following seven types based on their symmetries:
- horizontal axis
- vertical axis
- both horizontal and vertical axes
- rotational symmetry of 180 degrees about a central point
- rotational symmetry about a horizontal axis
- combine glide reflection and rotational symmetry of 180 degrees
- while some patterns involve glide reflection and horizontal rotational symmetry
Interestingly, every assertion mentioned in the section is backed by proof. For instance, instead of simply asserting the obvious 2D plane and the 3D space, the authors provide mathematical proofs and explanations.
I also liked how the authors have explored and presented the concept of dimensions using cartesian coordinates and vector spaces.
Cartesian coordinates allow us to define and explore dimensions by assigning numerical values to each coordinate axis. That is, by specifying a point’s coordinates along each axis – x,y and z- we can locate it uniquely in three-dimensional space. Specifically, cartesian coordinates are a system for specifying the positions of points in space.
While vector spaces provide a formal framework for exploring dimensions, as they can have any finite or infinite number of dimensions. Vectors in a vector space can represent various mathematical objects, such as points, displacements, forces, or other quantities with magnitude and direction.
In simple terms, vector spaces are more abstract than Cartesian coordinates and are not limited to representing points in space.

All the above concepts of dimensions converge to the next topic – the study of surfaces. And hence, the authors talk about the Euler’s Map Theorem.
As per the theorem, if we draw a network of n number of lines on a piece of paper, with a condition that no lines cross each other except at their ends. Then if we count the corners or vertices, subtract the lines, and add the spaces, we’ll always get 2. It doesn’t matter how we draw the network – this rule will always work. This also happens to be the “Magic Theorem”.
The “Magic Theorem”, as per the authors, is a significant result that relies on Euler’s characteristic and the classification of surfaces. Notably, it serves as a fundamental principle in the field of topology. A branch in mathematics which studies the properties of space that are preserved under continuous deformations, such as stretching, bending, and twisting, but not tearing or gluing.
Color Symmetry, Group Theory, and Tilings
Part II takes a different turn. It covers more abstract concepts such as color symmetry, group theory, and tilings. Although the book mentions that familiarity with group theory for this section is a must. Even readers with a solid grasp might struggle to stay engaged, particularly with the concepts of the group number function gnu(n), which counts the distinct abstract groups of order n. As mentioned, it’s best understood with a background in group theory.
However, the captivating illustrations including diagrams, animations, and interactive simulations continue to enhance the text’s visual appeal because of which I could pick up some cues as to what color symmetry and tilings mean.
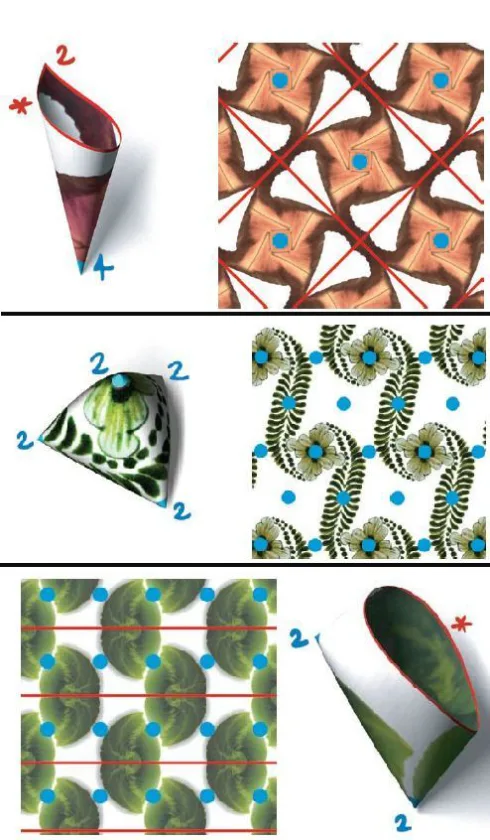
Tilings are the patterns which are formed by arranging identical shapes to cover a plane without any gaps or overlaps. They have intriguing mathematical properties. And are also studied extensively in mathematics, art, and architecture for their aesthetic appeal.
When examining tilings, color symmetry denotes a type of symmetry that maintains both the layout of the tiles and their designated colors. Basically, using a color symmetry operation on a colored tiling yields a tile layout with the same color pattern as the original arrangement. Below image can be used for visual aid.
Repeating Patterns in Other Spaces
Part III explores interesting topics including various shapes, symbols, and space. I’ll highlight a few that particularly caught my interest. But before that I want to share a quote, mentioned by the authors right at the beginning of the third and final section of the book.
“Part I of our book is accessible to those interested in mathematics but with no particular mathematical skills, while we expect readers of Part II to know some group theory (a first course suffices for all but a few tricky details). We expect that Part III will be completely understood only by a few professional mathematicians. Once again, however, much of it can be read with profit by some readers, and many more will enjoy inspecting our pretty pictures.” Pg. 217
I fall in the category of those who “enjoy inspecting the pretty pictures” 🙂 so here we go:
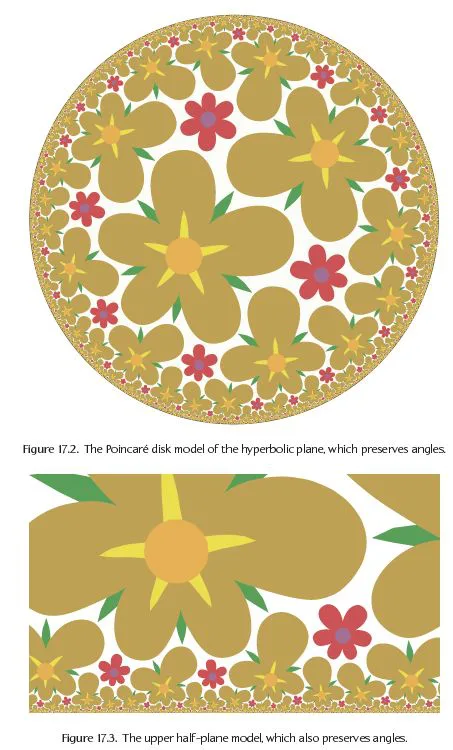
Repeating patterns in the hyperbolic plane – It refer to arrangements of shapes that exhibit certain symmetries under transformations in hyperbolic geometry.
Hyperbolic geometry deals with surfaces that have curves like a saddle or a Pringle chip. In this geometry, the lines aren’t straight, but they curve away from each other.
Unlike Euclidean geometry, which is flat and familiar, hyperbolic geometry is like exploring a world where everything is curvy and angles act differently. Therefore, repeating patterns can take on various forms due to the unique properties of the hyperbolic plane.
Archimedean polyhedral – Each vertex is surrounded by an identical combination of regular polygons. Thus, giving these polyhedra a high degree of symmetry. It includes the truncated icosahedron (commonly known as the soccer ball or buckyball) and the rhombicuboctahedron.
Catalan polyhedral – Its surface has all vertices equivalent but not all faces regular polygons. It includes forms like the rhombic dodecahedron and the triakis tetrahedron.
Generalized Schläfli symbols – They denote the number of sides (edges) of the faces of the polyhedron. In simple words, it provides a concise way to represent the arrangement of vertices, edges, and faces of a polyhedron.

Prime space groups – It is also known by the name of crystallographic space groups. They describe the repeating patterns of atoms or molecules in a crystal. They show how these patterns are arranged and repeated throughout the crystal lattice, giving each crystal its unique symmetry.
Composite space groups – They account for situations where the crystal structure exhibits additional symmetries beyond those described by the prime space group alone.
The 35 “Prime” Space Groups – They refer to a set of unique symmetrical arrangements that describe how objects can be organized in three-dimensional space.
In simple words, the 35 groups are like the basic puzzle pieces for understanding how crystals are put together. They help us understand the different ways atoms or molecules can organize themselves in a crystal. Just like puzzle pieces, they fit together to give us a clear picture of crystal structures.
Flat three-dimensional spaces – These refer to regions where the curvature is zero or negligible, similar to the flat surface of a table or a sheet of paper.
The 184 Composite Space Groups – Since, prime space groups are the fundamental building blocks, the composite space groups, on the other hand, are derived from these prime groups by combining them with additional symmetry elements, such as screw axes, glide planes, and inversion centers.
This effect gives rise to a wide variety of crystal structures and arrangements which is observed in nature.

Higher Dimensions
In addition to the above, the section also touches on fourth and higher dimensions. Visualizing 4D and higher dimensional objects can be difficult. The authors have tried their best with diagrams, projections, and even net representations (like unfolded boxes) to help readers grasp their structure. They have tried to explain how the following symmetries behave and manifest in higher-dimensional spaces:
Four-Dimensional Archimedean Polytopes – These are the regular, convex polytopes that exist, as the name suggests, in four dimensions.
Gosset’s Semi-snub Polyoctahedron – In simple words, it is created by cutting off some corners of a regular polyhedron, like an octahedron, in a particular pattern.
Groups Generated by Reflections – They are like sets of rules in math that come from flipping objects around in space. For instance, if we flip an object across lines or planes, those flips make up a group. This group happens to follow certain math rules. And so, it helps us understand how things can be symmetrical in geometry.
Hemicubes– These are like small sliced section of the main cube. In other words, a hemicube is like slicing a cube diagonally to have two equal parts. Then, each half is divided into smaller sections in a certain way. They fit into the broader context of polyhedral geometry and symmetry of course.

Takeaway
Even though “The Symmetries of Things” leans towards the mathematical side, it offers plenty of enjoyment for readers who aren’t deeply immersed in math. If you’re intrigued but worried it might be “too math-heavy,” don’t hesitate to give it a try. While there’s definitely a fair amount of math involved, it’s presented in a very approachable way.
After finishing “Surfing Through Hyperspace” by Clifford A. Pickover last year, I was fascinated by patterns, shapes, and dimensions. Now, diving into this book, I’m finding it takes my understanding of patterns and symmetry even further, which is truly exciting. The authors have made a profound contribution to the literature of mathematics with their work, and I’m incredibly grateful for it.